【洛谷日报】浅谈后缀数组算法

浅谈后缀数组算法

后缀数组(suffix array)是一个通过对字符串的所有后缀经过排序后得到的数组。
后缀数组同时也是后缀树的一个替代品，它比后缀树更好写，所以OIers通常会使用后缀数组，而非后缀树。

参考资料（转侵删）：

xminh的blog
后缀数组-Wikipedia
国家集训队2009论文
基数排序-百度百科
《算法竞赛入门经典》刘汝佳

前言

最近看到了一些将后缀数组的文章，看上去写的不错，便对后缀数组这个算法心生兴趣，学了之后发现，他写起代码来还是对萌新有一些难度的（比如说我），所以我想把自己在学习的过程中遇到的一些困难记录下来，以免大家也在此环节纠缠不清。嫌我啰嗦的就挑代码看吧。

一些约定&介绍

所谓后缀数组，数组大家都知道，那啥是后缀嘞？

一个字符串S，它里面有很多个子串，所谓子串，也就是字符串以任意字符为开头，再在它后面的任意一个字符结尾的字符串。之后以str[i,j](i<=j)来表示从S[i]~S[j]的字符串。

而后缀，则是子串里面特殊的一种，如果它的长度为n，下标以0位开头,那么j=n-1。z之后以suf(i)表示以i为开头的后缀

后缀数组(sa[])，就是处理这些后缀的排名。也就是说，如果把一个字符串里的所有后缀全都取出来(共n个)，再让他们以字典序排列，我们可以通过后缀数组来清楚地看到排第一、第二、第三……的后缀是从几开头的。

后缀数组，通常还会带有一个“附加产品”——名次数组(rk[])，这个数组，可以让人知道从i开头的后缀，在所有后缀中能排第几。

如图：

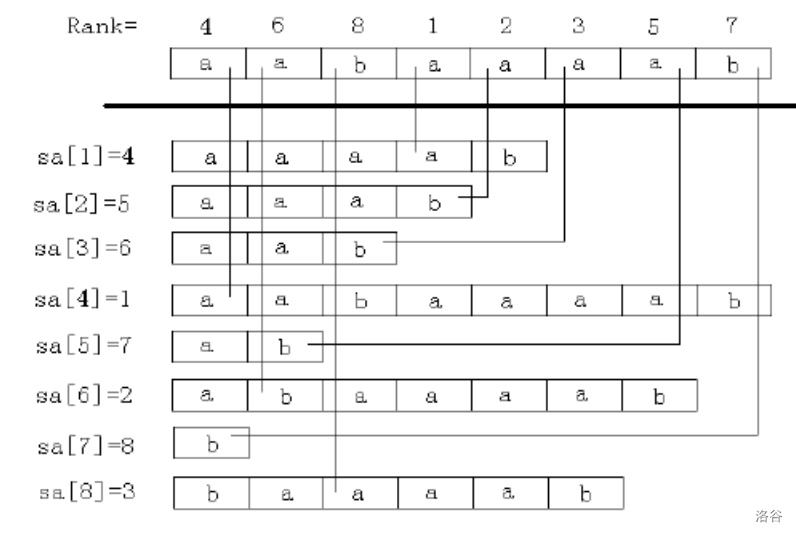
简单来说，sa[]记录的是 “排第几的是谁”，而rk[]记录的是 “它排第几”。

同时，我们还能发现一个性质：sa[rk[i]] = rk[sa[i]] = i。

理解了后缀数组到底是什么之后，我们就可以学习后缀数组的求法。

实现一个后缀数组

怎么求后缀数组，可以说是本文最主要，最重要的部分。我们有很多种求法。

$O(n^2 \log n)$ 做法

非常简单，就是最暴力的做法：把每个后缀当一个字符串，再将其扔进sort()里完事。sort()的复杂度是$O(n \log n)$，再加上字符串大小比较的$O(n)$总共就是 $O(n^2 \log n)$。这么暴力的东西谁都会写，当然也比正解要慢了许多。

$O(n \log n)$ 做法

一共有两种著名的求后缀数组的算法，我们先讲简单易学好理解的倍增算法。

倍增算法

好学归好学，关键难理解

刚才字符串暴力排序的复杂度之所以高，那是因为他直接横向地比较了每个字符串的大小，这样根本没有优化的空间和方法。但如果我们换个思路，纵向比较呢？

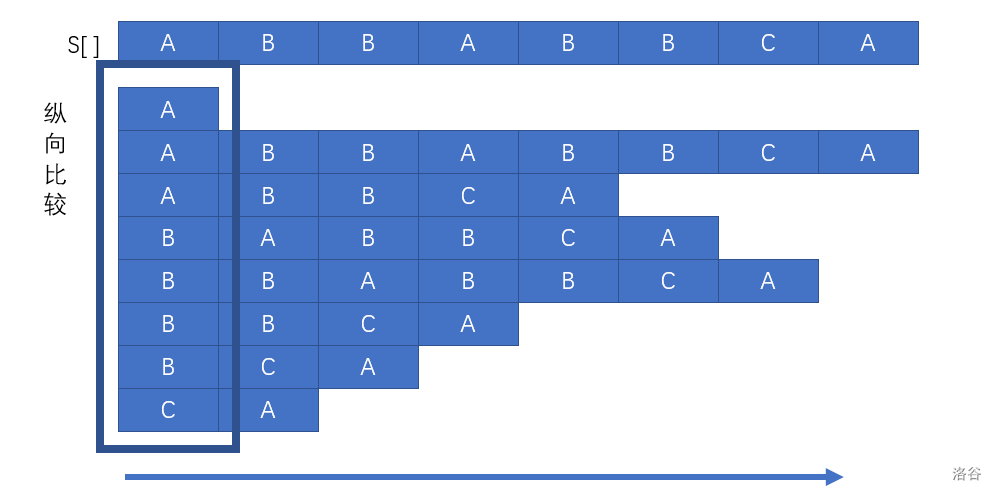
有人要说：这样做不是跟刚才一样吗？

但是其实不是，首先，我们抛弃了$O(n)$的排序比较，有更大的优化空间。第二，人是活的，我们可以将其稍加调整，不对其字符进行比较，而使用其字符所在的排名进行比较。如图：

每个字符串的第一个字符已经比较完毕，根据字典序比较的原则，接下来就应该比较第二个字符。当然，比较第二个字符的前提是第一个字符也要按照字典序排列。也就是说，我们形成了一个双关键字的排序。

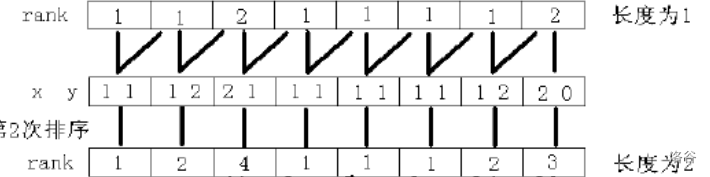
那接下来呢？比较第三个字符吗？并不是。倍增算法就体现在这里。我们会发现，其实应该将它们两两合并，变成4个关键字仍然不影响排序。但是，我们上一步已经两两合并了，也就是说，4个关键字，实质上只要管2个关键字，这就是倍增。接下来倍增为8，依然如此。

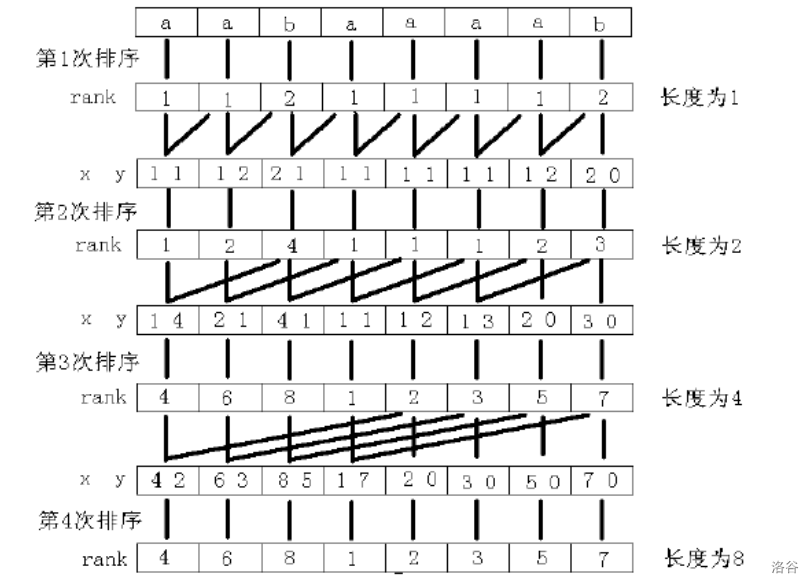
那么我们什么时候可以停止倍增呢？

要知道，如果像奥尔加团长一样不停下来的话，就会TLE，所以，当倍增数$>n$的时候，就可以停了。（因为所有第二关键字都是0）并且，如图所示，如果sa[]数组没有任何数字是相同的话，也可以提前停止。（因为第一关键字不出现相等的情况）。

不过，排序是$O(n \log n)$的，倍增一共$O( \log n)$ 次，咋就$O(n \log n)$呐？

要知道，字符的排序，有一个特性：最大值较小。因为字符数量有限，考虑所有数字和字母，最大的’z’也不过一百多。再加上特殊的双关键字排序，我们完全可以不用快排，而改用基数排序。

基数排序

基数排序就是把数据统统扔进桶里面的排序（
在执行基数排序的时候，我们要建一个数组，这个数组的没一个元素，就是所谓的“桶”。

例 ： 排序(1,2),(3,2),(1,3)，第一个数为第一关键字，第二个数为第一关键字。

1. 我们先按照第二关键字，一个一个把数据扔进桶里。

   	桶1	桶2	桶3
   无	(1,2),(3,2)	(1,3)

2. 将桶里面的东西全抽出来，不改变在桶内的数据，然后再按第一关键字扔进桶里。
   | | 桶1 | 桶2 | 桶3 |
   | ---- | --------------- | ------ | ------ |
   | (1,2),(1,3) | 无 | (3,2)|

再将其抽出来后，就是一个排完序的数组啦~

这样排序的正确性在于：我们第一次排完序之后，实际上就已经保证了同一第一关键字，第二关键字的相对顺序正确。这样，我们只要保持原来相对顺序不变，只管第一关键字排序就行了。这也是第一次排序是按照第二关键字的原因。

那么，我们先看一下基数排序的代码（单关键字，双关键字本质上就是做它两遍）：

//b数组：桶
for(int i = 0;i<n;i++)b[s[i]]++;
//++表示将一个数据放入桶
for(int i = 1;i<=m;i++)b[i]+=b[i-1];
//通过求前缀和的方法，将每一个桶内的东西排上名次
for(int i = n-1;i>=0;i--)sa[--b[s[i]]]=i;
//由于我们求得是sa[],所以b[s[i]]表示排名（刚才已经前缀和过了）而--的原因是为了消除并列的情况，i表示此后缀的标号。

不难发现，使用基数排序后，排序的复杂度达到了$O(n)$。再加上倍增所用的$O( \log n)$，总复杂度就是$O(n \log n)$。

思路都讲完了，接下来就上代码了。理解了思路不一定写的出代码，因为代码有很多细节需要考虑。

首先，是初始化的代码。初始化先使用基数排序，直接求出倍增之前的sa[]数组,顺便还能初始化一下x[]数组：

/*初始化阶段：基数排序*/
//m是桶的上限，也就是ascii码中最大的编号
for(int i = 0;i<n;i++)b[x[i]=s[i]]++;
for(int i = 1;i<=m;i++)b[i]+=b[i-1];
for(int i = n-1;i>=0;i--)sa[--b[x[i]]]=i;

接下来就到了倍增的环节。大家可能认为，每一次倍增就要进行基数排序两次（双关键字），其实不然。我们对第二关键字的排序结果是可以直接通过在初始化时的sa[]数组直接算出的：

for(int k = 1;k<=n;k*=2){//倍增的开头，k就是长度
    num = 0;
    //y[i]:记录第二关键字排序之后排第i位的对应x[]数组的下标是谁（有点拗口）
    for(int i = n-k;i<n;i++)y[num++] = i;
    //通过前几幅图的观察得知，数组中后k个数的y值都是0，肯定最小，所以排名肯定最高
    for(int i = 0;i<n;i++)if(sa[i]>=k)y[num++] = sa[i]-k;
    //sa[i]<k的，不可能成为一个第二关键词。在之后-k，是因为对应x[]数组

接下来，对第一关键字的基数排序：

for(int i = 0;i<=m;i++)b[i] = 0;
//初始化
for(int i = 0;i<n;i++)b[x[y[i]]]++;
//因为y[]指向的是x[]下标，它就顺理成章地成为了这次基数排序时x的下标,整个基数排序的过程相当于把i换成了y[i]
for(int i = 1;i<=m;i++)b[i]+=b[i-1];
for(int i = n-1;i>=0;i--)sa[--b[x[y[i]]]]=y[i],y[i]=0;
//y[i]=0可以顺便对y[]进行初始化

那么是不是排完一遍序，倍增的一个循环就结束了呢？当然不是。因为我们并没有更新x[]的值（y[]的值已经提前求出），所以，接下来就可以利用更新完的sa[]来更新x[]数组：

swap(x,y);//这里看似是交换，其实是利用已经初始化的y[]来建一个原有x[]的副本
num = 0;//归零
x[sa[0]] = 0;//排第一的人的排名是第一（废话）
for(int i = 1;i<n;i++)x[sa[i]] = (y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
//上面的for:如果他们的第一关键字和第二关键字都和上一名相同，他们本质上是同一排名。如果不相同，那么排名++
if(num==n)break;//num=n代表整个x数组内没有一个相同的排名，说明倍增可以停止了
m=num;//同时，整个数组的最大值就是num，不可能有更大的桶存在

好的！这就是求后缀数组的全部代码！接着，带上你的完整代码，去AC P3809吧！（注意数组范围，注意卡常）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int n,m;
char s[10001000];
//在定义数组的时候，有一个小细节，这里的y[]必须开两倍大小
int b[7501000],x[7501000],y[7501000],sa[7501000];

void SA(){
    int num;
    for(int i = 0;i<n;i++)b[x[i]=s[i]]++;
    for(int i = 1;i<=m;i++)b[i]+=b[i-1];
    for(int i = n-1;i>=0;i--)sa[--b[x[i]]]=i;

    for(int k = 1;k<n;k*=2){
        num = 0;
        for(int i = n-k;i<n;i++)y[num++] = i;
        for(int i = 0;i<n;i++)if(sa[i]>=k)y[num++] = sa[i]-k;
        for(int i = 0;i<=m;i++)b[i] = 0;
        for(int i = 0;i<n;i++)b[x[y[i]]]++;
        for(int i = 1;i<=m;i++)b[i]+=b[i-1];
        for(int i = n-1;i>=0;i--)sa[--b[x[y[i]]]]=y[i],y[i]=0;
        swap(x,y);
        num = 0;
        x[sa[0]] = 0;
        for(int i = 1;i<n;i++)x[sa[i]] = (y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
        if(num==n)break;
        m=num;
    }
    return;
}

int main(){
    gets(s);
    n = strlen(s);
	m = 128;
	SA();
    for(int i = 0;i<n-1;i++){
        printf("%d ",sa[i]+1);
    }
    printf("%d\n",sa[n-1]+1);
    return 0;
}

除了倍增算法，还有一种奇特的DC3算法，写起来很复杂，也快不了多少，个人认为OIer只要学倍增算法就够了。

后缀数组的应用

既然我们已经生成了后缀数组，那么它到底可以用来干什么呢？它可以用来做哪些题目呢？

LCP

所谓LCP，就是Longest Common Prefix,最长公共前缀。~~话说叫LC的怎么那么多：LCT,LCA,LCM,LCP…~~比如说：字符串abbaa与abaab的lcp就是2.因为他们的前两个字符相同。之后的$LCP(i,j)$函数中的i与j，表示的是它们在后缀数组sa[]中的的下标，这也是为什么我们刚才要求后缀数组的原因。

通过求sa[],我们可以求出它们两两之间的LCP，从而解决各种问题。那么这个LCP该如何求呢？

对此，我们可以证明几个小定理。（不需要可以跳过）：

显然的

LCP交换律：$LCP(i,j)=LCP(j,i)$
自己跟自己的lcp：$LCP(i,i)=len(i)=n-sa_i+1$

通过上述两条，我们继续推出：

（篇幅有限，对两条定理感兴趣的可以去xminh的blog阅读）

LCP Lemma

$LCP(i,k) = min (LCP(i,j),LCP(j,k)) (i \le j \le k)$
这个可以很容易的用图示感性理解：

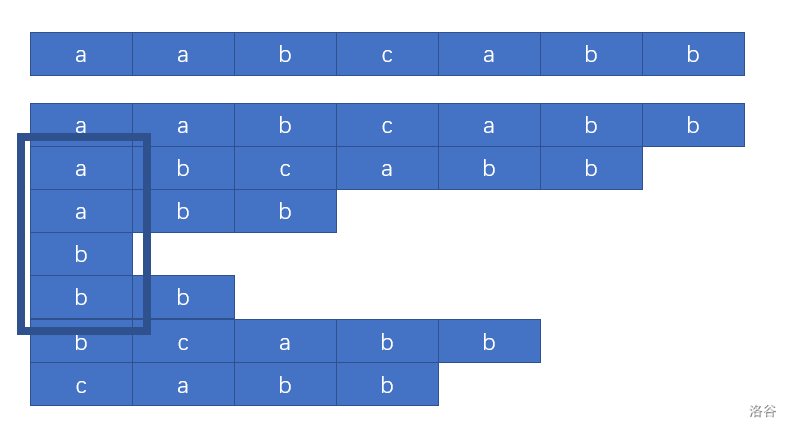
LCP Theorem

$LCP(i,k)=min (LCP(j,j-1))$ ( $1 < i \leq j \leq k \le n$ )

求出LCP的方法

知道了LCP Lemma和LCP Theorem了之后，其实是远远不够的。因为我们还是不知道求LCP的方法。如果使用暴力的话，那么求出所有lcp也需要 $O(n^3)$ ，这比求SA数组还要慢得多。所以不能这样，对此可以进行一些优化。

我们求LCP，其实并不需要求一个二位数组，而是使用一个数组height[]，来表示在sa[]中，相邻两个后缀的LCP。同时再建一个数组h[]作为辅助，h[i] = height[rk[i]] （写代码时并不需要建立h[]）。通过建这个数组，我们可以推一个最为重要的定理： $h_i \ge h_{i-1} -1$。这个就有必要证明一下了。

我们在sa[]数组里面找一个后缀，设它在原字符串的下标为i-1。在sa[]中的前面一个后缀，它在原字符串的下标为k。现在，把它们两个后缀的首字母都砍掉，它们就变成了i和k+1。

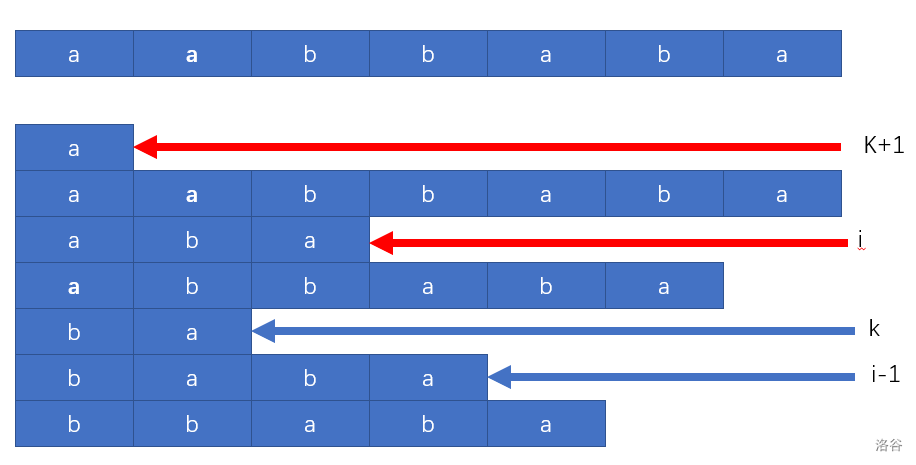
这张图我们也可以看出，当两者的首字母相同时，删除首字母后排名先后肯定也是不变的。而且，它们的LCP长度为h[i-1]-1。而根据LCP Theorem，我们可以知道，这个LCP长度是这个区间中最小的，因此 $h_i \ge h_{i-1} -1$

那么当两者首字母不同呢？那就更简单了，首字母不同，它们的LCP一定是0，不可能有比他更小的了。综上所述，$h_i \ge h_{i-1} -1$。

应用这个定理，可以排除很多情况，直接将复杂度降到$O(n)$。

接下来就是代码的实现问题了，直接上代码吧！

void height(){
    int k=0;//k可以看做当前的h[i-1]
    for (int i=0;i<n;++i) rk[sa[i]]=i;//这个在文章的开头就提到过
    for (int i=0;i<n;++i)  
    {
        if (rk[i]==0) continue;//height[0]肯定为0
        if (k) k--;//h[i] >= h[i-1]-1,所以直接从h[i-1]-1开始枚举
        int j=sa[rk[i]-1];//j是i相邻的一个后缀，求height
        while (j+k<=n && i+k<=n && s[i+k]==s[j+k]) k++;//枚举它们的LCP
        ht[rk[i]]=k;//k就是LCP的值
    }
}

我们求出了height数组！那么如何利用height，来求LCP呢？

根据LCP Theorem，我们知道，这可以转化为一个RMQ问题，使用st表(Sparse-Table，稀疏表)来解决这个问题。感兴趣的可以移步关于st表的博客。

例题

学会了如何写一个后缀数组以及LCP之后，我们就可以利用它们做几道题了。

P2408 不同子串个数

给你一个长为N的字符串，求不同的子串的个数。

这道可以说是一道SA最简单的裸题了。算法标签里面没标sa一般我们找不同子串，都是按照长度枚举之后暴力去重。但是我们运用后缀数组，就可以实现$O(n)$去重。

具体是这样的：我们知道，对于每一个后缀，它都能产生自身长度个前缀。而所有后缀的所有前缀，其实就是这个字符串的所有子串。然后怎么去重呢？这就要使用height[]数组了。我们知道，相邻两个后缀的LCP大小，其实就是这两个后缀的子串中，有几个是重复的。因此我们只要把所有子串的个数，减去height[]数组的每一项，就可以了。

而且，所有子串的个数，我们还可以使用公式$T_i = \frac{n(n+1)}{2}$来$O(1)$求得，那就更方便了！

核心代码如下：

/*抄是过不了的，要看清本题数据范围*/
long long ans=n*(n+1)/2;
    for(long long i = 0;i<n;i++){
        ans-=ht[i];
    }
    cout<<ans<<endl;

UVA11107Life Forms

给n个字符串，求长度最大字符串，要求在超过一半的字符串中出现。

这道题有很多的解法，先介绍一下在蓝书里面的后缀数组解法。

首先把所有字符串拼起来。将这个大字符串求后缀数组和height[]。然后，我们可以进行二分答案来判定这个“长度最大字符串”的长度l。每当碰到一个height[]中的元素小于这个所判定的长度，就给它分段。如图所示。

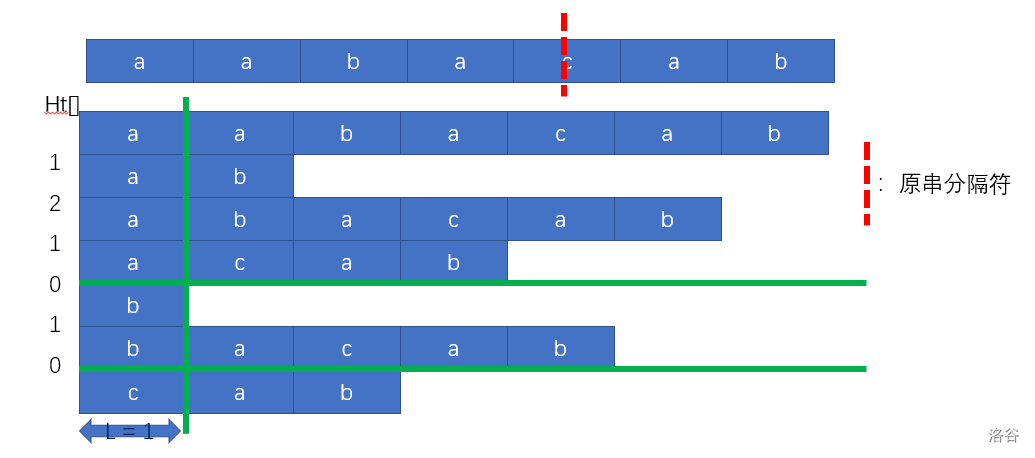
（绿色横线表示分段）

如果说都一段中，有超过n/2个原串，那么说明这个长度l是合法的。

但是万一有两个不同原串拼在一起变成了一个新串导致lcp错误怎么办？没有关系。我们可以在每两个原串中，放一个从来没有出现过的字符，这样子就能使两个不同原串强制分段，lcp=0.比如说有3个串：abcd,acbd,cdba，我们这样子拼起来：abcd-acbd_cdbaJ（最后一个字符也要加）。

结语

好了，这就是关于后缀数组的全部内容了，可以在评论区留言。后缀数组的功能远不止这些，我也只是挑了2道较易理解的题。希望对大家有所帮助~祝大家在OI之路上顺利，各个吊打我！/cy

本文写于2020年。然而现在的我已经完全不会后缀数组了，令人感叹。